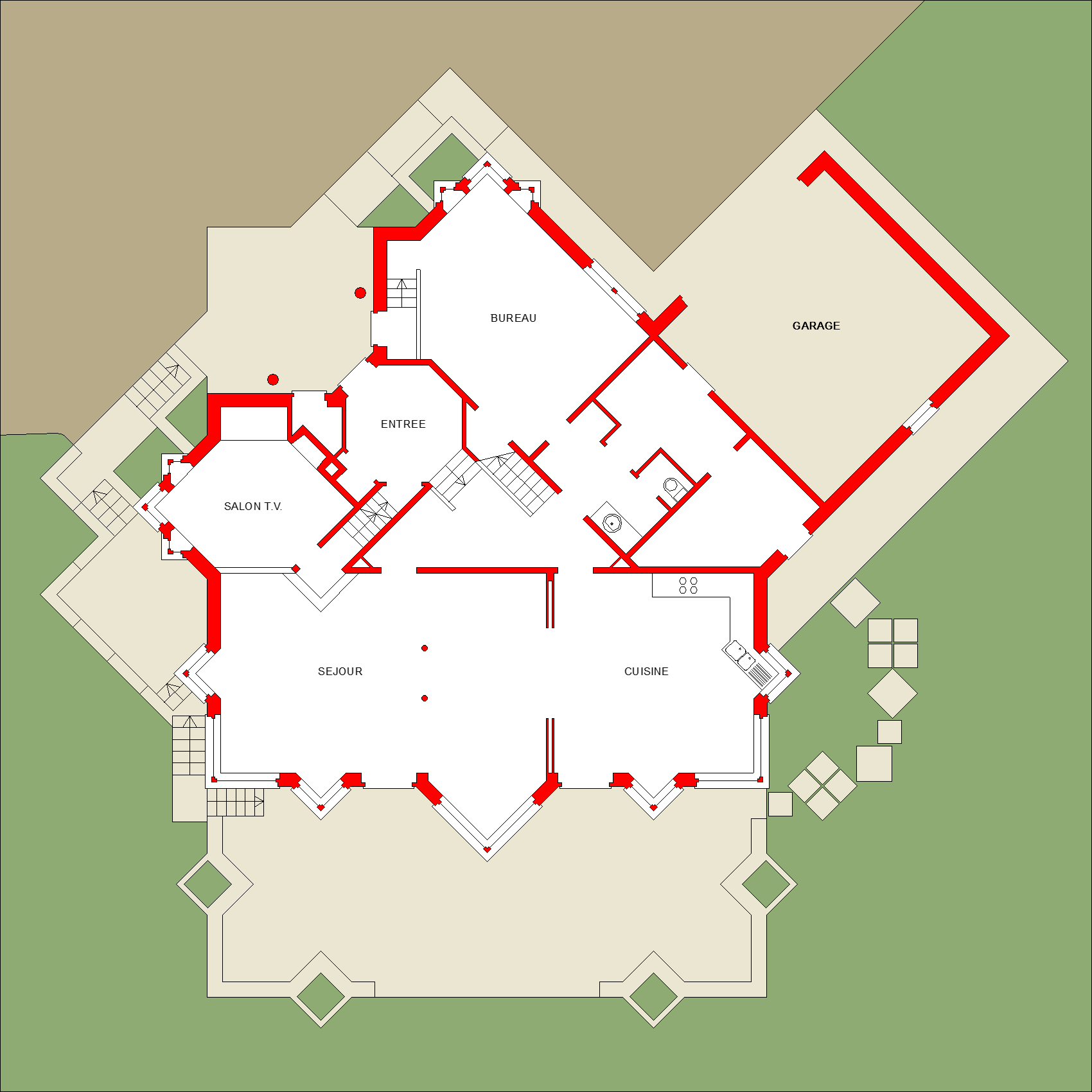
FRACTAL HOUSE

Lillois.

Before being a designed or built form, the Fractal House was a family for which 500m² of diverse spaces would harbor their p^rivate and professional lives. The chosen place is 20 km away from Brussels.

THE FORM : A PALLADIAN FRACTAL.

We wanted here to bring together the classical reference and the local tradition through a simple, clear and logical constructive expression. The counterpoint between a careful brick masonry and the structural accents in a noble material (white concrete) illustrates this approach with a Palladian inspiration.
The site is retired from the street and stands above the neighbourhood on the South side. The house is very open towards the South : garden terrasse and living rooms; the North is there for the parking of cars and the entrance. The North side is pivoted 45° so as to offer a more accomodating aspect to the visitor.

This double orientation aroused the adoption of a dual system of frames shifted by 45°. And then came the idea to give them a formal coherence with a geometric pattern which would encounter the intellectual and aesthetic preferences of the owner : a fractal curve.
Fractals are lines folded in self-convolutions so complicated and compact that it is impossible to isolate a fragment which, however small, could be seen as a measurable segment. The classical line is a mathematical object of dimension one (two for the surface, three for the volume); the fractal line is a special being with a dimension between one and two. We talk about the fractal dimension, a non-intuitve notion but more rigorous than the traditional dimension as an integer.
A singular group of fractal lines is noticeable for its aesthetic productivity, the self-similar fractals : every part of the line contains a series of others which reproduce it at a smaller scale. One of those has been chosen here as a matrix for the plan : a variant of the so-called Koch curve recursively generated through the insertion in the middle of every segment a right angle turned 45°, like a chinese hat : . Starting with a square, the first three stages of the fragmentation look like this :

FRACTALS THEORETICAL and FRACTALS CONCRETE.

Of course, a geometric pattern does not make architecture, and it is later, in the sunsequent work of conciliation with the other -functional and structural- determinations that the whole gets resolved.

In the present case the path towards the material and the detail presented a particular interest.
On the contrary of euclidean forms, like the circle or the square, which you could perceived at first glance, fractal curves are not intuitive. Touching them the mind may feel a discomfort which is no small cause of their reputation as mathematical 'monsters'. To build or perceive a fractal, the mind must proceed through recurrence. At every stage the image shirks : any segment just imagined gets fragmented. The figure exists only in the flow of a logical time. This evanescence of the shape plays an essential role in its architectural exploitation : you find in its very nature an incompleteness which thrives to its fullfillment through the definition of its constructive or functional details.

In our example an option is very early chosen concerning the openings for doors and windows : the elementary operation of substitution of a chinese hat for a segment the segment becomes a plain wall and the inserted angle becomes a corner window. The layout gets to look like this outline :

From form to design : the form gets inhabited by functional constraints -a dialog which is not uninteresting.

Two problems appear : 1. Our fractal is until now a 2-D drawing; how does get to become a 3-D obhect ? 2. Fragmentation is in theory endless; how does this happen for an architectural plan ? Seeking the answers to these questions shall give us a particularly interesting lighting on two fundamental and entangled values of architecture , proportion and scale.

For the transit to the third dimension, an a priori solution seems to be a simple upward extrusion, each segment becoming a facet.

There is still to define the heights, for the windows for instance. Couldn't we simply extend to the third dimension the principle of reduction operatiog in the plan, and organise the volumes in decreasing series, a little like nested Russin dolls ? This way we would give the problem of proportions a radical solution : the relation of the small to the large being treated as a simple homothetic ration.

But in the real world where we live the vertical dimension is not at all of the same character as the horizontal dimensions : it is the direction of rain, of gravity, of the active position of our body related to which perception is dependant. For the determination of the levels of window thresholds and lintels for instance, the freedom of geometric creation is strictly limited by material contingencies.: it gives a frame to the visual field for adults and children. We shall thus be led to give the windows a proportion inversely slender to its size, meeting here a law of life which binds the shape to the size.

The application of the mechanical proportional reduction down to the tiny is no problem for the mathematical thing, and that makes the originality of the fractal concept : it is a scaleless being, and our imagination explores it from the huge to the minuscule in a unchanging landscape. But if we take the fractal as a model for a material object, our diving towards the infinity gets tangled up in the bounds of matter to its expanse. The size of a door is related to our size, the size of a window frame is not related to the size of the window. And the fractal thing must be manufactured; if it is made of bricks, there can be no fragmentation beyond the brick.

The rule of diminution must be inflected and curbed, the proportion of the getting larger when the segments get smaller.

Axonometric view on the South, garden side.

This interference in the pure play of proportion is the architectural criterion of Scale, which says that no shape should be considered independently of its size. Geometry gets lost. Compromise is necessary.

The development in height tells the struggle between euclidian and fractal geometries. The roofs are compliant to the tarditional economy of slope and right angle, and as we go down the spaces get unfolded in fractal outgrowths.

Crowned by a glass canopy, the core of the house is the strairway which gives a right angle structure to the activities.

The central light well
(Colours are indicative of altitude, like in the relief geographix maps.)

On the entrance side, the fractal excrescences are reduced, so the façade may be in close contact with the central core.

Vue axonométrique de l'Ouest, côté entrée.

SCULPTURE, ANOTHER DIMENSIONAL TRANSCENDANCE

The architect asked sculptor Therese Chotteau to intervene on places where our sensibility expects the special signifier of rupture which is ornament. These points which capture the glance and the mind are the disruptions of structure and function, pillars and doors.

A pair of columns frames the main entrance, with a masonry arch above; between the concrete and the bricks, the transition is made by an ornamental capital.

If fractals are a way to include the infinite in a finite whole, the sculptural image within an architectonic system gives us another modality of this paradox. There is here also a scale rupture, but it is inherent to image. The depth of space is the one of figuration, and its temporality is narrative.

The sculptor resumes the thematic of geometry, a fund of figures with immemorial symbolic and emotional resonances. Each of the two reliefs represents a scene contrasting human beings and polyedras. The latter seem indifferent to the passions of which they are the objects, curiosity of the child, dream of the mathematician or speculation of the architect.